

(Esta entrada participa en la Edición 5.4 Martin Gardner del Carnaval de Matemáticas, cuyo anfitrión es el blog Gaussianos.)
PRIMERA PARTE
 Hay un gran revuelo días antes de que comience el Mundial de Fútbol de Brasil 2014, ya que el Comité Organizador ha decidido introducir una modificación de última hora.
Hay un gran revuelo días antes de que comience el Mundial de Fútbol de Brasil 2014, ya que el Comité Organizador ha decidido introducir una modificación de última hora.
Quieren conseguir que participen más países que los 32 ya clasificados para la fase final del torneo. Hay muchísimas selecciones que han quedado fuera del Campeonato.
Dada la enorme expectación que genera este Mundial, y la decepción de numerosos países por no haber podido clasificarse, los organizadores del Mundial han decidido ampliar el número de selecciones que podrán competir en el mismo.
Dada la enorme expectación que genera este Mundial, y la decepción de numerosos países por no haber podido clasificarse, los organizadores del Mundial han decidido ampliar el número de selecciones que podrán competir en el mismo.
El calendario de competición establecido inicialmente para los 32 países era el siguiente: una primera ronda con sistema de liguilla con 8 grupos de 4 países, de los que se clasifican los 2 primeros de cada grupo.
Los 16 equipos así clasificados se enfrentarán entre sí por el sistema de eliminación directa hasta la final, en la que el vencedor se llevará la Copa del Mundo.
Sin embargo, si quieren añadir más países, y que el campeonato no se prolongue excesivamente, deberán adoptar necesariamente un nuevo sistema de competición, descartando los grupos iniciales y realizando partidos eliminatorios desde un principio.
Además, dada la disponibilidad de los distintos estadios de fútbol y los problemas de logística que se pueden derivar de esta modificación, han determinado incrementar los 51 partidos que inicialmente se preveía disputar con el antiguo sistema, como mucho hasta los 60 partidos.
 El Comité Organizador ha organizado una reunión con varios expertos del Departamento de Matemáticas Aplicadas del Ministerio de Educación.
El Comité Organizador ha organizado una reunión con varios expertos del Departamento de Matemáticas Aplicadas del Ministerio de Educación.En esta reunión, el presidente del Comité expone al resto de asistentes el par de problemas que se presentan:
- El primero de ellos es determinar el número máximo de selecciones que pueden participar si se celebran un total de 60 partidos. Queremos que vengan al Mundial la mayor cantidad posible de países. Así, por una parte, tendremos más visitas de turistas procedentes de los países participantes, y por otra parte, tendremos más ingresos por los derechos de televisión de los que decidan verlo desde casa.
- El segundo es analizar de cuántas formas distintas se puede realizar dicho torneo con eliminatorias directas.
- ¿A qué te refieres exactamente?
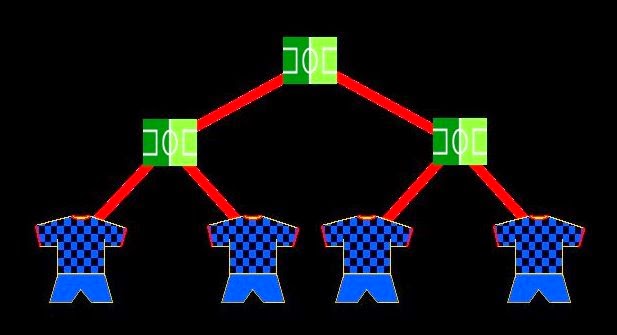
- Me refiero a que el campeonato se puede disputar de muchas formas. Por ejemplo, podemos establecer que haya 8 cabezas de serie, y que el resto de países compitan entre sí hasta que queden sólo 8 equipos que se enfrenten con ellos en octavos de final. Así, si representamos los partidos a disputar como pequeños estadios rectangulares de color verde, y a los equipos participantes con una camiseta y un pantalón de fútbol de color azul, el esquema de competición quedaría así:
- O que haya sólo 4 cabezas de serie, y que el resto se vayan eliminando hasta que queden sólo 4 selecciones, que se enfrenten con ellos.
- O que haya solo 1 cabeza de serie (el país organizador, claro está), y que el resto se eliminen hasta que quede sólo uno, y juegue con nosotros la final. En fin, todas las posibles variantes que se os ocurran.
- Entendido. Pero... no va a ser posible... Es mucho trabajo... para tan poco tiempo como queda.
- No quiero excusas. Venga, pongámonos manos a la obra, y mañana nos reunimos nuevamente aquí.
Tras la reunión, el jefe del Departamento de Matemáticas Aplicadas se muestra muy preocupado por los problemas planteados ¿Podrías ayudarle?
SEGUNDA PARTE
Al día siguiente, vuelven a encontrarse los expertos matemáticos con los miembros del Comité Organizador.
- Vamos a intentar resolver la primera cuestión. ¿Qué me contáis? ¿Cuál es el máximo número de países que podemos convocar si se celebran 60 partidos?
- Bueno, creo que lo mejor va a ser confeccionar un cuadro, como en los torneos de tenis. Vamos a representar la final con un pequeño campo de fútbol, como dijimos anteriormente, y de él partirán 2 líneas hacia los dos equipos que van a disputarla. Ya tenemos 1 partido.
- Ahora vamos a sustituir las camisetas por otros dos campos de fútbol, que representarán los 2 partidos de semifinales. De cada uno de ellos volverán a partir 2 líneas hacia los equipos que las disputan. Y si sumamos estos 2 partidos al de la final, ya contamos con 3 partidos en total.
- Seguimos así con los 4 partidos de cuartos de final, los 8 partidos de octavos de final, y los 16 partidos de dieciseisavos de final. Ahora tenemos un total de 1+2+4+8+16 = 31 partidos.
- Nos quedan 29 partidos para completar los 60 que queremos que se disputen en el campeonato. Así que no se pueden celebrar todos los 32 partidos de treintaidosavos de final, ya que tendríamos un total de 31 + 32 = 63 partidos. Podéis contar los campos de fútbol en el esquema, para comprobar que son 63.
- Nos sobran 3 partidos. Así que eliminamos 3 partidos, haciendo que haya 3 equipos que se clasifiquen directamente para dieciseisavos de final.
- Ahora vamos a contar los equipos que participarán en el torneo: son las camisetas azules cuelgan como hojas en los extremos de cada rama.
- Es verdad, el esquema del torneo parece un árbol. Bueno, después de contarlos, me salen 61 camisetas, esto es, que que pueden participar hasta 61 países, ¿verdad?
- Cierto, será así siempre que el torneo se organice con este esquema de competición. Pero, ¿y si manejamos unos 'árboles' distintos al que hemos confeccionado? Si queremos que haya 8 cabezas de serie que comiencen su participación en octavos de final, o si queremos que haya 4 cabezas de serie, respetando siempre que sean 60 partidos los que se celebren, los árboles serían los siguientes:
- ¿Qué pasaría ahora? ¿Participarían de esta forma más o menos países? ¿Y si se nos ocurren otros árboles diferentes de los que hemos pintado?
- Pues en estos dos ejemplos también cuento 61 países, pero no sé qué ocurriría con el resto de árboles que podríamos formar...
- Pues en estos dos ejemplos también cuento 61 países, pero no sé qué ocurriría con el resto de árboles que podríamos formar...
- Siempre serían 61 países, aunque para demostrarlo recurriremos a un procedimiento singular.
- Vamos a contar los países según queden eliminados y se vayan yendo a su casa. En todos los partidos de eliminación directa habrá siempre un perdedor, que ya no jugará más partidos. Sólo tenemos que pensar que en 60 partidos habrá 60 países ‘perdedores’, a los que tendremos que sumar el que gane la final, que también se irá a su casa, pero más contento. Por tanto, siempre habrá 61 países, independientemente de la forma que adopte el calendario de competición.
- O podemos verlo de otro modo: si, en cada partido que hemos representado con un campo de fútbol, pensamos que el equipo que gana el encuentro y pasa a la siguiente fase ocupa la mitad más oscura, mientras que el perdedor ocupa la mitad pintada con verde más claro, podemos comprobar que en 60 partidos hay 60 mitades más claras, correspondientes a los 60 equipos eliminados, a los que hay que sumar el equipo que ha ganado el torneo, y que siempre ha ocupado la zona oscura del campo. En total, 61 equipos. Y dará lo mismo el ‘árbol’ de competición que formemos.
- Además, si aún no os queda claro, podéis ver el fenomenal artículo: ¿Cuántos partidos hay en un torneo de tenis? de José Cárlos Gámez en Matemáticas Digitales.
- Pues es verdad. Así que ya podemos dar por resuelto el primer problema de averiguar el máximo número de países que pueden participar.
- Ahora vamos a ver la segunda cuestión: ver de cuántas formas distintas se puede organizar el campeonato. Dicho de otro modo, tenemos que evaluar los distintos árboles que podemos confeccionar para organizar el campeonato con 61 países.
- Bueno, no parece muy difícil. Vamos a empezar con un campeonato sin equipos. Con cero equipos, no se podría organizar ningún campeonato, ¿verdad?
- Ahora pensemos en un campeonato con un solo equipo. Es muy fácil. Sólo hay una forma de hacerlo: le damos el trofeo al equipo, y ya está.
- Con 2 equipos, ambos se disputarían la copa jugando la final. Sólo habría una forma de organizarlo.
- Correcto.
- Con 3 equipos, también sólo hay una forma posible de organizar el evento: primero se enfrentan dos equipos entre sí, y luego el ganador juega con el tercer equipo, ¿no?
- Efectivamente. Pero, si en vez de enfrentar en primera ronda al primer equipo con el segundo, hacemos que se enfrenten el primero con el tercero, o el segundo con el tercero, entonces tendríamos otros 2 esquemas de competición, ¿no?
- No. Es cierto que los equipos que se enfrentarían serían distintos, pero el esquema de competición sería el mismo: primero juegan dos, y el vencedor juega con el equipo restante. De momento, lo que nos interesa es averiguar cuántos cuadros de competición distintos se pueden confeccionar y decidirnos por uno de ellos. Luego ya veremos la forma de colocar a cada una de las selecciones dentro de dicho esquema, ¿vale? Así que los seguimos pintando del mismo color a todos los equipos, ya que no los queremos diferenciar.
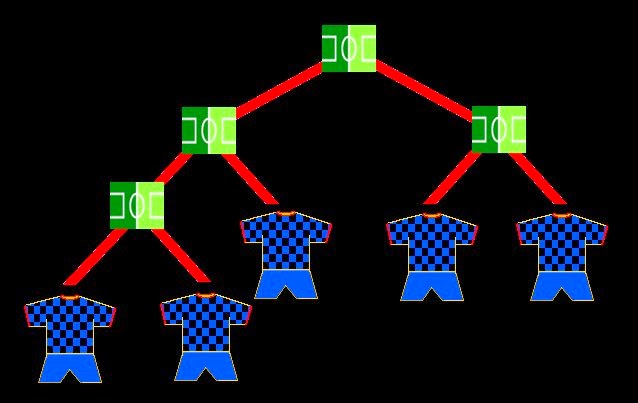
- Perfecto. Entonces vamos a trabajar ahora con 4 equipos. Lo más normal es hacer que se enfrenten entre ellos en 2 semifinales, y que los ganadores pasen a la final.
- Pero existe otra forma de enfrentarlos, eliminándose de uno en uno:
- Así que con 4 equipos, tenemos 2 árboles distintos. Vamos a ver con 5: hay 3 posibles maneras.
- Con 7 equipos podemos formar 11 árboles distintos. Con 8 construimos 23 árboles y con 9 podemos diseñar 46 árboles. Pero cada vez resulta más difícil ir dibujando las diferentes opciones. Creo que de esta forma no llegaremos a ninguna parte...
- A lo mejor deberíamos buscar alguna fórmula para calcular cuántos árboles diferentes se pueden formar con 61 competidores. Para ello, vamos a estudiar la serie que llevamos hasta ahora, a ver si podemos deducir cuáles serán los siguientes términos.
- Pues no parece que los números obtenidos obedezcan a ningún tipo de secuencia matemática. Tal vez deberíamos buscar en internet una solución para nuestro problema.
- Sí, pero primero tenemos que definir exactamente qué es lo que buscamos.
 - Bueno, estos árboles que estamos dibujando se denominan ‘grafos’ en términos matemáticos. Y como tienen una forma jerárquica, que simula la de un árbol (o una raíz), también en matemáticas y en informática se les conoce por el nombre de 'árboles'.
- Bueno, estos árboles que estamos dibujando se denominan ‘grafos’ en términos matemáticos. Y como tienen una forma jerárquica, que simula la de un árbol (o una raíz), también en matemáticas y en informática se les conoce por el nombre de 'árboles'.
- Además, son unos árboles muy especiales, ya que de todos los estadios pequeñitos (que llamaremos nodos) que representan los partidos parten 2 líneas (ramas o hijos). No puede haber un partido en el que se enfrenten más de 2 equipos, así que hablamos de árboles binarios, ni tampoco se puede jugar un partido con un solo equipo, por lo que se trata de un árboles estrictamente binarios.
- Por otra parte, nos da lo mismo el orden de las distintas ramas, ya que nos estamos fijando en la estructura del árbol, y no nos importa de momento quiénes jueguen los partidos, como ya hemos dicho antes. Así que estamos hablando de árboles estrictamente binarios no ordenados.
- Ya solo tenemos que utilizar el buscador de internet, poner ‘cuántos árboles estrictamente binarios no ordenados se pueden formar’ y esperar los resultados...

- Pues no hay muchos resultados. Además, no me parece que se ajusten a lo que estamos buscando. A lo mejor no estamos enfocando bien el problema.
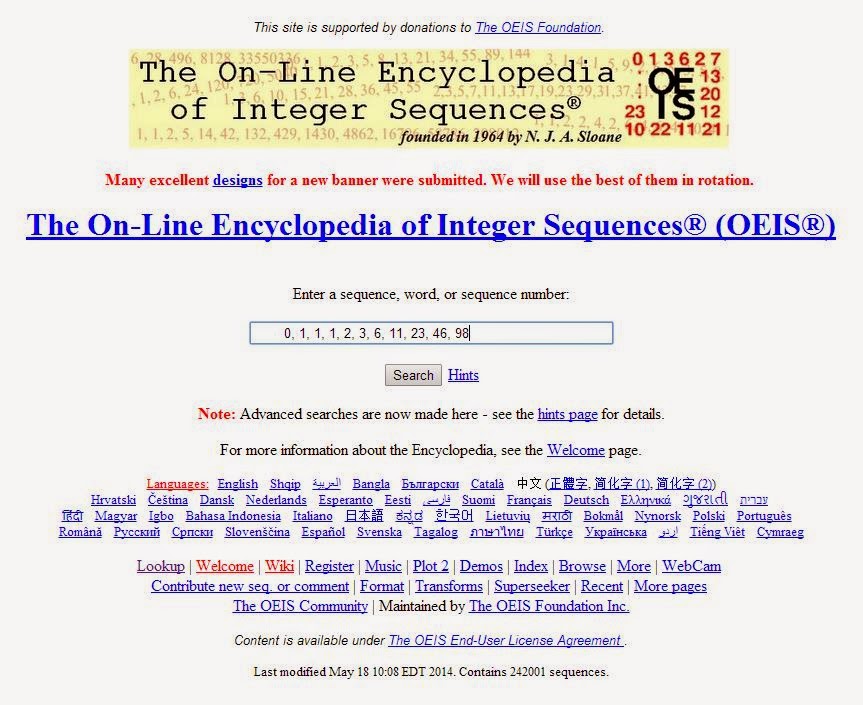
- Deberíamos retomar nuevamente la serie de árboles que habíamos calculado previamente:
0 1 1 1 2 3 6 11 23 46 98
- Y la introduciremos en esta utilísima página web, que reconoce todo tipo de series a partir de sus términos:
 - ¡Ahá! Aquí tenemos la solución: se trata de la serie A001190 de Wedderburn-Etherington. Podemos comprobar que, dentro de las utilidades descritas para esta serie, figura la de calcular la cantidad de posibles calendarios de competición diferentes que se pueden formar con un número determinado de participantes.
- ¡Ahá! Aquí tenemos la solución: se trata de la serie A001190 de Wedderburn-Etherington. Podemos comprobar que, dentro de las utilidades descritas para esta serie, figura la de calcular la cantidad de posibles calendarios de competición diferentes que se pueden formar con un número determinado de participantes.
- Ahora solo tenemos que ir al apartado donde T. D. Noe elabora una tabla con los 200 primeros términos de la serie, y obtener el resultado para 61 equipos:
844206159208807054529
- ¡Vaya número! Vamos a ponerle los puntos, para que nos hagamos una idea más precisa de su magnitud.
844.206.159.208.807.054.529
- ¡Más de 844 trillones de árboles distintos! ¡Ni en la selva amazónica hay tanto árbol!
 - Parece un número bastante grande. Y dijimos que queríamos estudiar todos los casos para ver qué sistema adoptamos, ¿no? Pues vamos a tener que trabajar mañana y noche, creo.
- Parece un número bastante grande. Y dijimos que queríamos estudiar todos los casos para ver qué sistema adoptamos, ¿no? Pues vamos a tener que trabajar mañana y noche, creo.
- Bueno, pensemos un poco. Si uno de nosotros le dedica 1 minuto a cada ‘árbol’, y no come, ni duerme, ni descansa, necesitará un total de 160.617.610.995.447 años.
- Habrá que poner a trabajar a todo el Departamento.
- Qué va, aún en el caso de que todos los brasileños (más de 201 millones de personas) se empeñasen en esta tarea, tardarían 7.989.625 años en conseguirla.
- Bueno, pues ya que a casi todo el mundo le gusta el fútbol, ¿qué tal si solicitamos la ayuda de toda la población mundial?
- En ese caso, se tardarían 221.987 años en estudiar durante 1 sólo minuto cada una de las posibles formas de organizar nuestro campeonato de 61 equipos.
- Por cierto, supongo que te acuerdas de cuando comenté que no nos interesaba diferenciar los distintos equipos, y que debíamos centrarnos tan sólo en la estructura del campeonato, ¿verdad?
- Sí, aunque no entendí muy bien por qué.
- Vamos a retomar el tema por un momento. Tenemos 61 equipos, así que queremos saber las distintas formas en que podemos ordenarlos. En Matemáticas, hablamos de las permutaciones que se pueden dar en un conjunto de 61 elementos.
- Así es. Y es fácil de calcularlas. El primer equipo que elijamos puede ser cualquiera de las 61 selecciones. Para cada una de ellas, el segundo equipo lo escogeremos esta vez entre los 60 restantes. Para cada una de estas combinaciones de 2 equipos, tendremos ahora 59 equipos entre los que elegir al tercer país. Y así sucesivamente.
- Por tanto, el número total de permutaciones de los 61 países será igual a:
- Por cierto, supongo que te acuerdas de cuando comenté que no nos interesaba diferenciar los distintos equipos, y que debíamos centrarnos tan sólo en la estructura del campeonato, ¿verdad?
- Sí, aunque no entendí muy bien por qué.
- Vamos a retomar el tema por un momento. Tenemos 61 equipos, así que queremos saber las distintas formas en que podemos ordenarlos. En Matemáticas, hablamos de las permutaciones que se pueden dar en un conjunto de 61 elementos.
- Así es. Y es fácil de calcularlas. El primer equipo que elijamos puede ser cualquiera de las 61 selecciones. Para cada una de ellas, el segundo equipo lo escogeremos esta vez entre los 60 restantes. Para cada una de estas combinaciones de 2 equipos, tendremos ahora 59 equipos entre los que elegir al tercer país. Y así sucesivamente.
- Por tanto, el número total de permutaciones de los 61 países será igual a:
61 · 60 · 59 · 58 · ..... · 3 · 2 ·1 = 61!
- Efectivamente, para abreviar utilizamos la expresión 'factorial de 61', que representamos con el símbolo de admiración. Y si realizamos el cálculo, obtendremos el siguiente resultado:
61! = 5,0758 · 10 83
- O sea, un cinco seguido de 83 cifras más. Si el número de árboles ya te parecía enorme (8,4421 · 10 20), imáginate cómo lo será éste. Y si multiplicamos el número de árboles con el de las formas de ordenar los distintos países dentro de ellos, obtendremos un precioso número:
- ¡Cuarenta y dos mil ochocientos cincuenta gúgoles de formas distintas de organizar nuestro campeonato! Hay que recordar que un gúgol es mayor que el número de átomos de hidrógeno que existen en el universo conocido...
- Uff. Entonces creo que lo mejor será emplear el sistema tradicional: 29 partidos de treintaidosavos, librando a tres países de esta primera ronda, y eliminatorias completas desde dieciseisavos.
4,2850 · 10 104 = 42.850 · 10 100
- ¡Cuarenta y dos mil ochocientos cincuenta gúgoles de formas distintas de organizar nuestro campeonato! Hay que recordar que un gúgol es mayor que el número de átomos de hidrógeno que existen en el universo conocido...
- Uff. Entonces creo que lo mejor será emplear el sistema tradicional: 29 partidos de treintaidosavos, librando a tres países de esta primera ronda, y eliminatorias completas desde dieciseisavos.
- Los 3 países exentos serían Brasil, y otros dos.
- ¡Claro!
- Pues venga, vamos a decidir ahora a qué países invitamos a participar para completar el cuadro de 61 equipos. Y también deberíamos pensar en organizar algo original para la ceremonia de apertura. ¿Qué tal si regalamos unos balones que llenen todo el estadio?
- De acuerdo. Pero antes, si alguien está interesado en este tema de las topologías arbóreas, aquí dejo unos enlaces para profundizar en el mismo: Matemáticas para computadora, Estructuras de datos, Árboles.
- Y más abajo os dejo otros enlaces, por si os gustó la historia y queréis compartirla vuestros amigos.
- Hasta la vista. ¡Y que gane el mejor!
































No hay comentarios :
Publicar un comentario