El fin de año no sería igual sin los confetis, unas espirales que se convierten en hélices cuando las lanzamos al aire. Hay miles de ejemplos de curvas matemáticas que nos acompañan sin que apenas nos demos cuenta: espirales de Arquímedes, espirales logarítmicas, espirales de Fermat, clotoides... si hablamos de dos dimensiones. Y hélices cilíndricas, cónicas, esféricas... si pensamos en tres dimensiones. Antes de las 12 campanadas, varias de estas curvas se cruzarán en el camino de Pepe Vitruvio.
(Esta entrada participa en la Edición 6.9: El conjunto de Cantor del Carnaval de Matemáticas, cuyo anfitrión es, en esta ocasión, ::ZTFNews.org)
PRIMERA PARTE
 Los equipos del AS Mónaco y del Las Vegas Mobsters van a disputar un partido benéfico el día de Nochevieja, a favor de las víctimas del método de Montecarlo.
Los equipos del AS Mónaco y del Las Vegas Mobsters van a disputar un partido benéfico el día de Nochevieja, a favor de las víctimas del método de Montecarlo.
Los jugadores se disponen a saltar al terreno de juego para comenzar a realizar el calentamiento, cuando el delegado del club se da cuenta de que no han sacado los balones.
El utillero ha cogido unos días de vacaciones, así que van a recoger las llaves del almacén de material a su despacho, pero en su lugar, en vez de las llaves, han encontrado un disco navideño colgado de la percha. Intentan llamarle por teléfono, pero no hay forma de dar con él.
Se trata de una persona a la que le gustan los acertijos, por lo que el detalle del disco puede que no solamente represente su felicitación del nuevo año a sus compañeros, sino que además suponga algún tipo de pista para dar con la ubicación de las llaves.
 Pepe Vitruvio había acudido al estadio para ver el partido, así que el presidente le invita a bajar con él a los vestuarios para ver si pueden solucionar el problema.
Pepe Vitruvio había acudido al estadio para ver el partido, así que el presidente le invita a bajar con él a los vestuarios para ver si pueden solucionar el problema.
- ¡Vaya, un disco de U2! ¡New Year's Day! ¡Qué canción tan hermosa para festejar el año nuevo!
- Sí, pero sería aún más hermoso si en su lugar hubiera unas llaves. Con el disco no podemos abrir la puerta del almacén donde guardamos los balones.
- Y, ¿qué queréis que haga yo? Sería mejor que avisarais a un cerrajero.
- Ya, pero es que hoy es Nochevieja, y no hay ningún establecimiento abierto. Cuando queramos dar con alguien que quiera venir a abrir la puerta, ya se habrá pasado la hora del comienzo del partido.
- Yo no sé nada de abrir puertas...
- Pero sí de acertijos. Y estamos convencidos de que lo del disco se trata de uno. Además, al utillero le encantan las Matemáticas, así que seguro que tiene que haber alguna relación.
SEGUNDA PARTE
 - ¿Habéis probado a escuchar el disco, para ver si contiene algún mensaje grabado en el que indique el lugar donde ha dejado las llaves?
- ¿Habéis probado a escuchar el disco, para ver si contiene algún mensaje grabado en el que indique el lugar donde ha dejado las llaves?
- Afortunadamente conservamos todavía un viejo tocadiscos en el club. Lo hemos utilizado, y lo único que se escucha es la canción. Lo raro es que haya dejado un disco de vinilo, y no algo más moderno como un CD o un formato digital.
- Puede que esa sea la pista.
- Ah, ¿sí?
- Es posible. ¿Vosotros sabéis cómo está grabado un disco de vinilo?
- Pues no.
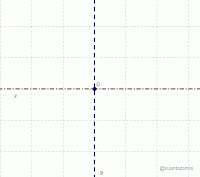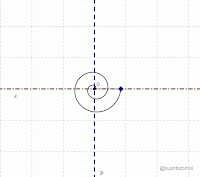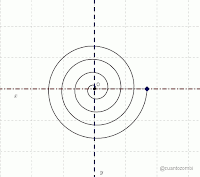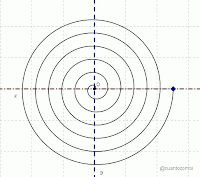
 - A diferencia de los discos compactos, en un disco de vinilo la información está grabada en una sola pista. Se trata de una espiral, que la aguja lectora va recorriendo desde el borde del disco hasta su centro.
- A diferencia de los discos compactos, en un disco de vinilo la información está grabada en una sola pista. Se trata de una espiral, que la aguja lectora va recorriendo desde el borde del disco hasta su centro.
- Así que se trata de un solo surco, ¿no?
- Efectivamente. Este tipo de curva tiene una denominación especial en Matemáticas. Se le llama espiral de Arquímedes, ya que este antiguo sabio griego la describió en sus tratados.
- ¿Por entonces ya grababan la música en discos?
- No. Arquímedes la utilizó para sus estudios sobre la cuadratura del círculo.
- ¿Y sólo vale para eso?
- Qué va. Tiene múltiples aplicaciones. Se usa en los mecanismos de los compresores de aire acondicionado, en ciertas pruebas para el diagnóstico de enfermedades neurológicas, para calcular las concentraciones de bacterias, o para temas realmente importantes como contar los metros de papel higiénico que contiene un rollo, por ejemplo.
- Ya veo. Me imagino que las fórmulas que se utilizarán para su descripción serán muy complejas, ¿no?
- Depende. Si la definimos en coordenadas polares (r,θ), nos queda una expresión muy sencilla:
r = a + b·θ
- La fórmula define lo alejado (r) del origen que está cada punto de la curva, en función de las vueltas que vaya dando (θ) y de un coeficiente (b), que conforme más grande sea, mayor será la distancia entre las vueltas de la espiral.
- Pues no era tan complicado. Pero creo que estamos dando vueltas al asunto al igual la espiral de Arquímedes, sin llegar a ninguna conclusión.
- Bueno, creo que deberíamos buscar algún sitio del estadio donde podamos encontrar otra espiral de Arquímedes.
- Hmmm. No se me ocurre.
- Pues a mí sí. Justo en la entrada he visto un magnífico árbol de Navidad. Me he fijado en la disposición de las luces, y he visto que formaban una espiral de Arquímedes perfecta.
- Ah, ¿sí?
- Bueno, no exactamente. Se trataría más bien de una hélice, ya que es una curva continua que se desarrolla en tres dimensiones. Pero si observamos el árbol desde arriba, y proyectamos la hélice en sólo dos dimensiones, veremos que las luces están dispuestas según la espiral de Arquímedes.
- Bueno, no exactamente. Se trataría más bien de una hélice, ya que es una curva continua que se desarrolla en tres dimensiones. Pero si observamos el árbol desde arriba, y proyectamos la hélice en sólo dos dimensiones, veremos que las luces están dispuestas según la espiral de Arquímedes.
- El utillero.
- Bien, pues ya nos vamos acercando a la solución.
- Pero, ¿dónde puede haberlas escondido? ¿Colgadas de una rama?
- No creo. Quizás estén dentro de alguna de las bolas que adornan el árbol. Si os fijáis, todas ellas tienen un número.
- Sí, pero ¿en cuál estarán? No tenemos tiempo de romper todas las bolas para ver si dentro de alguna de ellas están las llaves.
 - No nos ha dejado más pistas, salvo el disco con la espiral de Arquímedes. Así que deberíamos centrarnos en ella. A esta espiral también se la conoce por otro nombre: ruleta de Arquímedes...
- No nos ha dejado más pistas, salvo el disco con la espiral de Arquímedes. Así que deberíamos centrarnos en ella. A esta espiral también se la conoce por otro nombre: ruleta de Arquímedes...
- ¡Ah! Ahora que lo mencionas, recuerdo que antes de trabajar para el club, el utillero estuvo empleado como crupier del Gran Casino. Quizás haya algún tipo de relación con la ruleta que dices.
- Es posible. La ruleta es un juego inventado por el matemático Blaise Pascal, quien además creó sus normas en el siglo XVII, sin que éstas hayan variado sustancialmente desde entonces. La novedad más importante introducida fue la de incluir, junto a los 36 números existentes, rojos y negros, por los cuales los jugadores pueden apostar, un número extra, el cero, exclusivo del casino, con el que éste consigue sus beneficios.
- Dado que él trabajó como crupier en el casino, quizás deberíamos abrir la bola con el número 37.
- ¡Qué número tan feo!
- No hay números feos, y menos éste. Es un número fascinante ya que, además de ser primo, es divisor de todos los números repdigit de tres cifras.
- ¿Números repdigit?
- Sí, números en los que se repite siempre la misma cifra: 111, 222, 333...
- ¡Qué número tan feo!
- No hay números feos, y menos éste. Es un número fascinante ya que, además de ser primo, es divisor de todos los números repdigit de tres cifras.
- ¿Números repdigit?
- Sí, números en los que se repite siempre la misma cifra: 111, 222, 333...
- Pues es verdad: ¡aquí están las llaves! Id enseguida a sacar los balones del almacén para que se pueda disputar el encuentro.
- Y nosotros vamos al palco, a abrir unas botellas para celebrar la resolución del problema y para brindar por todos nuestros seguidores y desearles que tengan un ¡Feliz Año Nuevo!

Si la entrada os supo a poco, podéis profundizar más sobre su contenido en estos magníficos artículos: Historia de la ruleta, Introducción a las espirales, La espiral de Arquímedes, Coordenadas polares y cartesianas.
Y, sobre todo, no os olvidéis de dar una vuelta por el Carnaval de Matemáticas y votar la historia que más os guste. Allí encontraréis unos excelentes artículos matemáticos de los que disfrutaréis con su lectura.







CUANTA ENSEÑANZA, CAPACIDAD Y AÑOS DE ESTUDIO. GRACIAS
ResponderEliminarCUANTA INTELIGENCIA, CAPACIDAD INTELECTIVA Y MAESTRÍA EN LA ENSEÑANZA. CONCIBIENDO CONOCIMIENTOS BÁSICOS EN SOLUCIONES APARENTEMENTE COMPLEJAS.
ResponderEliminarMUCHAS GRACIAS